Fourier Transformation (FT)
Data analysis
By Miroslava Cuperlovic-Culf
September 16, 2023
Basic idea of FT is to represent complex phenomena as a linear combination of simpler phenomena – in order to try and solve complex problem as a linear combination of solutions of simpler problems. Complex function decomposition can be done with series of sines and cosines as simpler functions – called Fourier series. If the original function has a repeating pattern, represented and decomposed into sines and cosines – then function can be said to have frequencies, represented within sines and cosines. Pretty much anywhere there is a signal in time that needs to be transformed into frequency FT finds use. Computationally or naturally. As an example – eye lens does a FT of the light into frequency components and places those onto retina; ear – takes a sound signal, pulls apart frequencies and transfer this info.
French Baron Jean-Baptiste-Joseph Fourier put this natural process into mathematical formula in the early 1800s – while studying heat transfer around iron ring attaching ship’s anchor to a chain. This was such a novel concept at the time, and really such a complex calculation for manual performance that FT didn’t become all-powerful and useful tool that it is today until 1960’s - computers and Fast Fourier Transform developed by James Cooley and John Tukey.
Fourier transform (FT) formula, provides a rigorous way to determine components of a complex system.
FT is a mathematical method used to transform function between domains by decomposing complex function in one domain into its constituent frequencies and amplitudes as the other or inversely synthesize, recreate function from its transformation components.
In mathematical notation FT is:
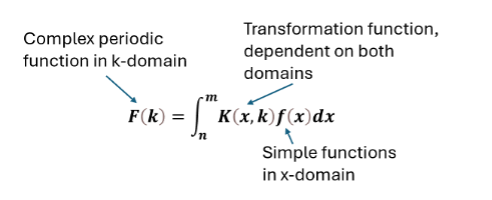
In other words - FT is a way of decomposing any (periodic) function into a series of waves with different amplitude, frequency, and phase. Integral over a series of these waves will bring us back to the original function. This opens many possibilities for pulling apart functional representation of different things - from signal processing (EEG, ECG), spectroscopy (MRI, NMR, FTIR) or spectrometry (FTMS) to crystallography. FT has a major role in data processing, denoising, sequence analysis, as a replacement of self-attention in natural language processing models inside transformers.
The Fourier transform in it most often seen application separates frequencies components of a temporal signal – i.e. it converts complex temporal signal to simpler subcomponents defined by their frequencies. Key to this is that any complex signal can be rewritten as a sum of components represented as set of simple sinusoids – in order words – if enough sinusoids, with different frequencies, phases and amplitudes are combined they can add up to almost any complex signal. In the case of time - to frequency- domain conversion FT converts a time function into a sum of sine waves with different frequencies, amplitudes, and phase shifts. In this case FT – transforms time domain signal showing intensity of some kind as a function of time into a frequency domain showing power spectrum of frequencies.
Few requirements to make disentangling of components possible are:
- Components and filters pulling them out have to be independent;
- Filters have to collect all possible ingredients from the function;
- Components can be recombined into the function prior to transformation.
Fourier transform can be done in few different ways, flavours:
- Discrete - DFT – because usually time course is measured at some time intervals,
- Continuous - FT – because sometimes time intervals are infinitesimally small and can be approximated to 0,
- Fast – FFT – because sometimes calculation time is of the essence.
| Infinite | Finite | |
| Continuous time | Fourier Transform
|
Fourier Series
|
| Discrete time | Discrete time Fourier transform
|
Discrete Fourier transform
|
| Continuous frequency - ω | Discrete frequency - k |
Based on: https://ccrma.stanford.edu/~jos/sasp/Fourier_Transforms_Continuous_Discrete_Time_Frequency.html
Fast Fourier Transform (FFT) combines discrete Fourier transform with faster processing for highly efficient application.
Formulas shown in the table can pull out sine functions that are combined in a signal and determine their individual frequencies. In fact – ANY continuous signal in the time domain can be represented by a unique and unambiguous series of an infinite number of sin functions.
Some very important numbers to keep in mind when doing Fourier transformation particularly Discrete and Fast Fourier transformation:
- Sampling rate is the average number of samples, measurements, obtained in 1 second.
- Nyquist rate is the maximum frequency that can be obtained with FFT. It is equal to half of the sampling rate of the instrument.
These numbers define what is possible when doing FFT: range of frequencies that can be determined depends on the sampling rate, i.e. how often are measurements in the time domain taken. Nyquist’s sampling theorem states that at least two points are needed to measure frequency and thus only frequencies that are less then half of the sampling rate can be accurately measured. This logically makes sense – without at least two points per cycle the wave can not be accurately imagined.
As an example, if sample property is measured ever 1ms, i.e. frequency of sampling is 1000 Hz then the maximum frequency that can be observed is 500 Hz. All frequencies higher then 500Hz would be insufficiently sampled and their estimated frequency would be lower then actual value.
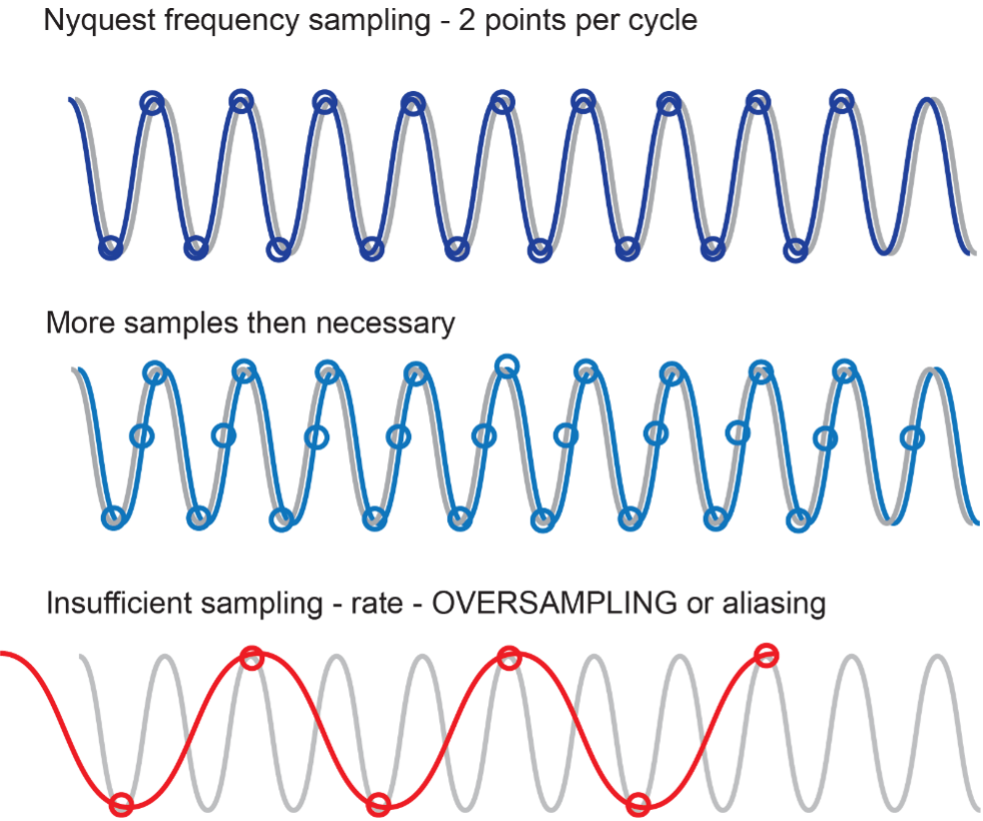
Figure shows differences in frequency that FT would determine based on the available sample measurements. In gray is the actual oscillation event, dots show measured points, blue or red are calculated oscillations
Some important properties of FT
FT is linear – sum of two functions leads to sum of their FTs
If:
Then:
FT frequency shift property – multiplication of function with complex sin wave of some frequency leads to frequency shift in FT
FT time shift property
FT time reversal property – going back in time leads to negative frequency
FT time scaling property – stretching over time has a specific effect of frequency:
FT convolution property - If two functions are convolved in the time domain then their FT is a product of two original:
FT can be performed on the complete signal - for example in the NMR where complete FID is Fourier transformed to give complete spectrum – so one function in the time gives one set of functions in the frequency domain for the whole period.
If function is changing over time, as for example in the EEG analysis, FT can be performed on time bins, giving frequencies in different time periods – i.e. for each frequency providing time course that comes from FT of time bins. Nothing different about FT here, just performed on bins, subsets in the signal.
In molecular sequence analysis where finding repeating patterns is of interest, for example in DNA sequence analysis, FT is used to find patterns, to find frequency of pattern repeats, to provide information about the change in patterns or to cluster groups of patterns. So signal is not intensity but the sequency for example letter appearance. The rest is the same.
In image analysis – FT can be used for denoising – doing FT first, selecting frequencies of interest, removing the rest and then doing inverse FT can lead to a much cleaner image.
A very nice example of FT of sounds is provided on this free site: https://academo.org/demos/spectrum-analyzer/
Of course FFT, DFT are available in all numeric methods and mathematical programming languages, free as well as commercial. Popular algorithmic solution is provided in https://www.fftw.org/. Pretty much every spectroscopy or signal processing software includes FFT or DFT protocols.
FFT is mathematics behind the autotune application that can make anybody sound half decent. Here FT pulls out frequencies from the sound and adjusts them to desired pitch – frequency while also removing, cleaning out any noise. How much is this cleaning of noise and pitch adjustment done can make sound more or less natural.